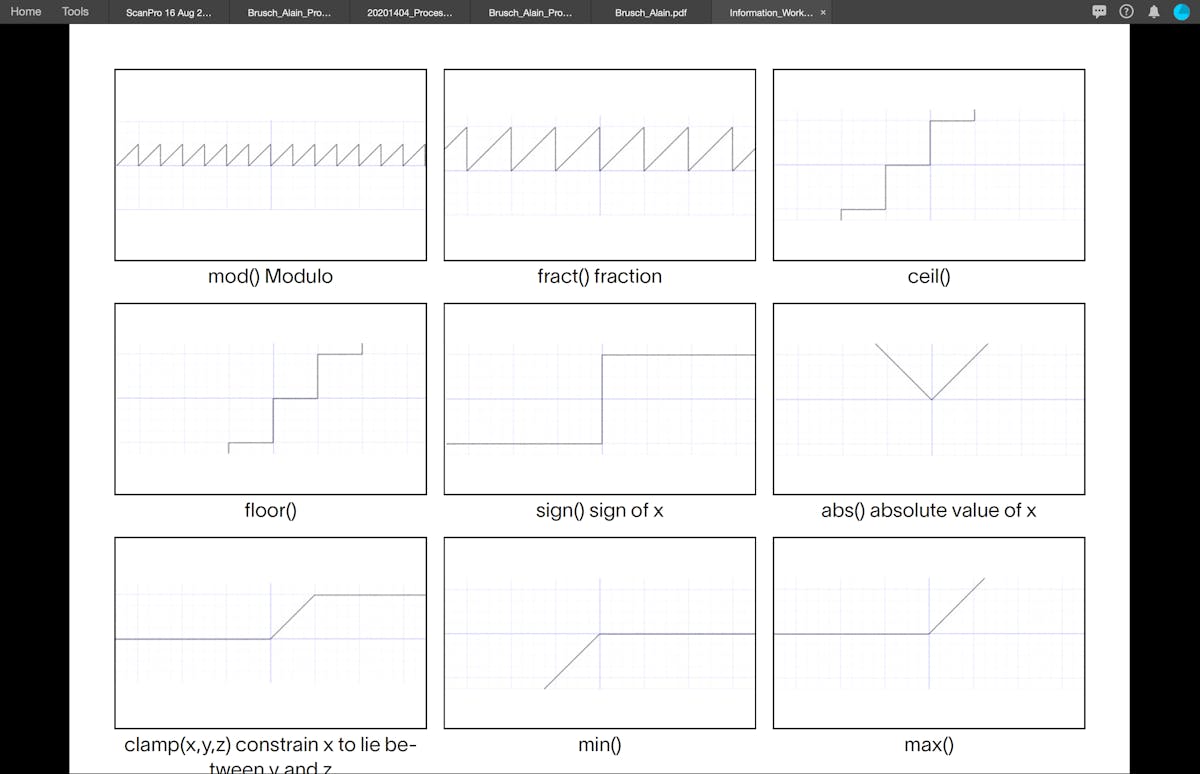
Advanced Shaping FunctionsGolan Levin (2006) built incredible documentation for functions that createmore complex shapes, which are of great value to my thesis. It is quite easyto transport these functions to GLSL and they proved to be an excellent base tostart building one's functions (Gonzalez Vivo & Lowe, 2015 in the Book of Shaders.
• Polynomial Shaping Functions
• Exponential Shaping Functions
• Circular & Elliptical Shaping Functions
• Bezier and Other Parametric Shaping Functions
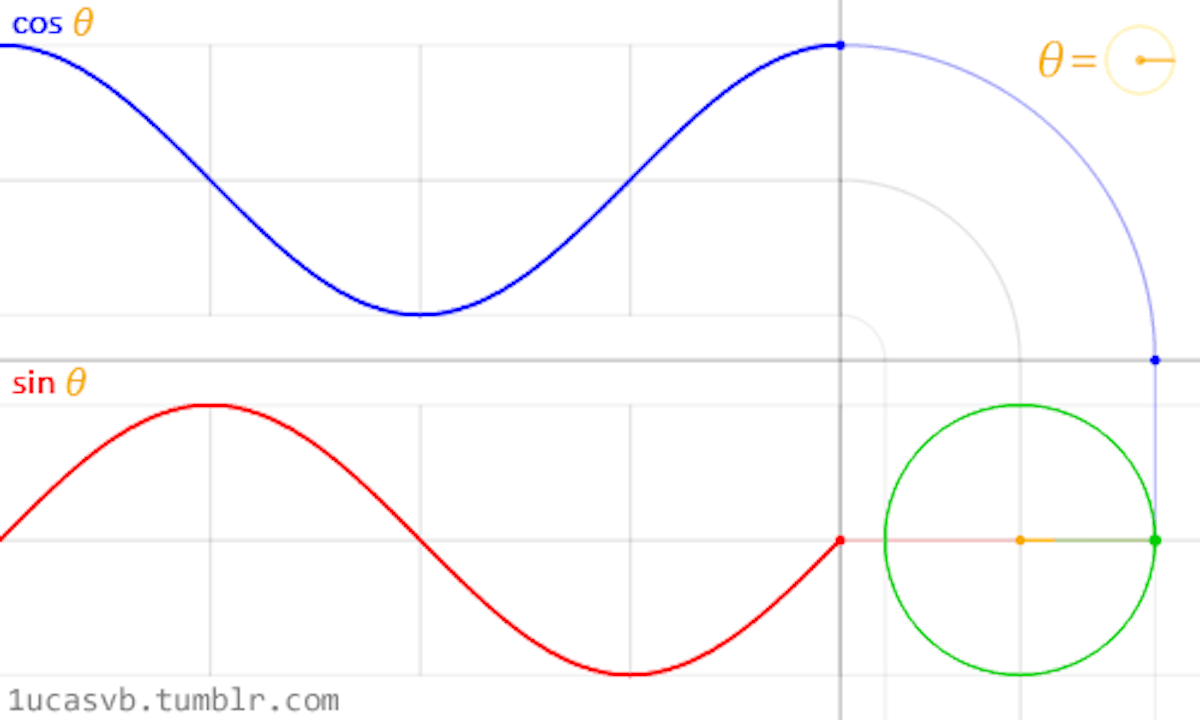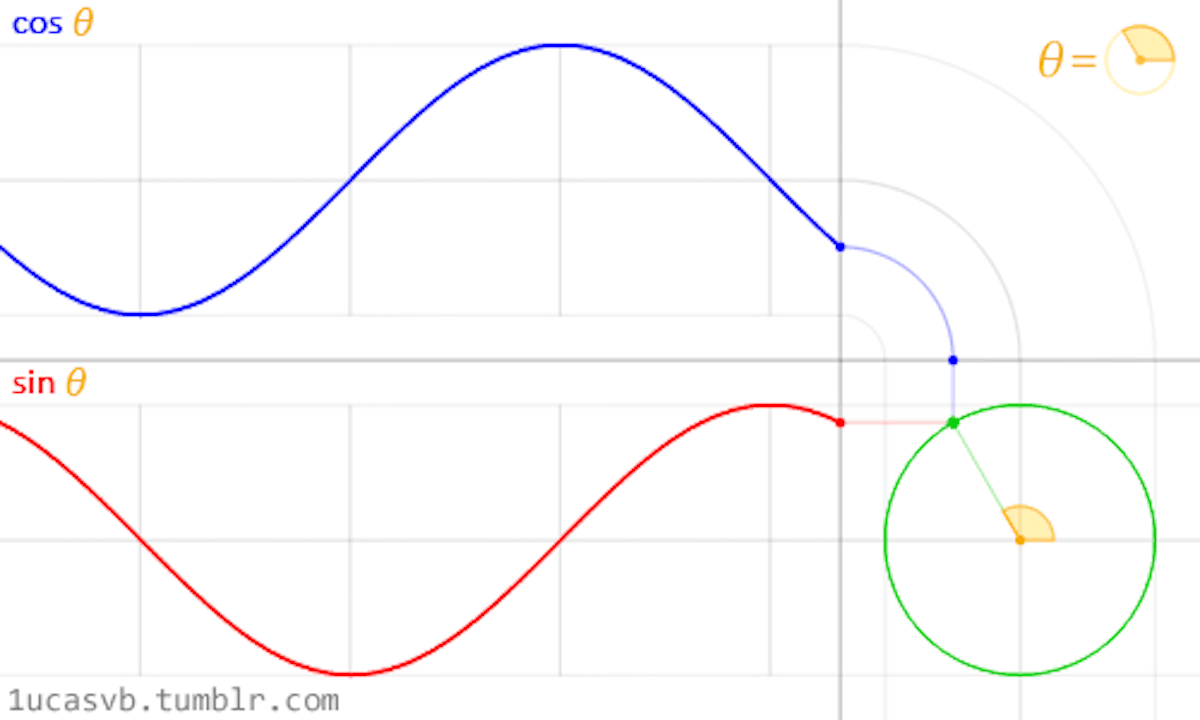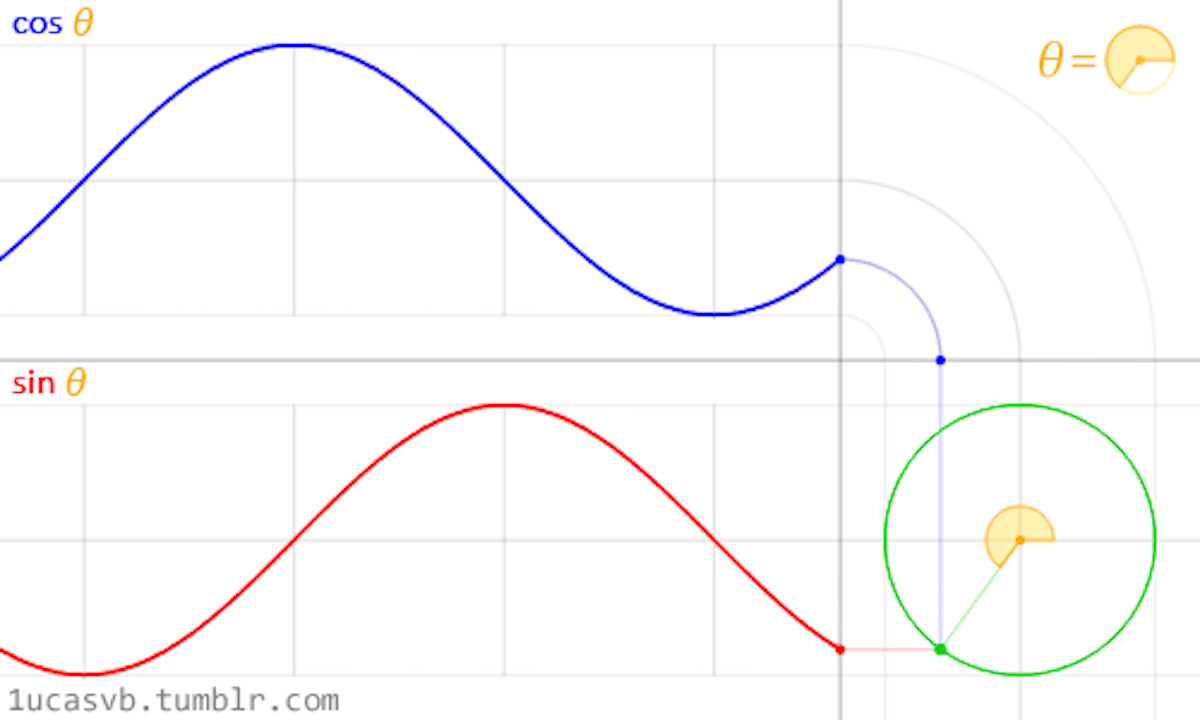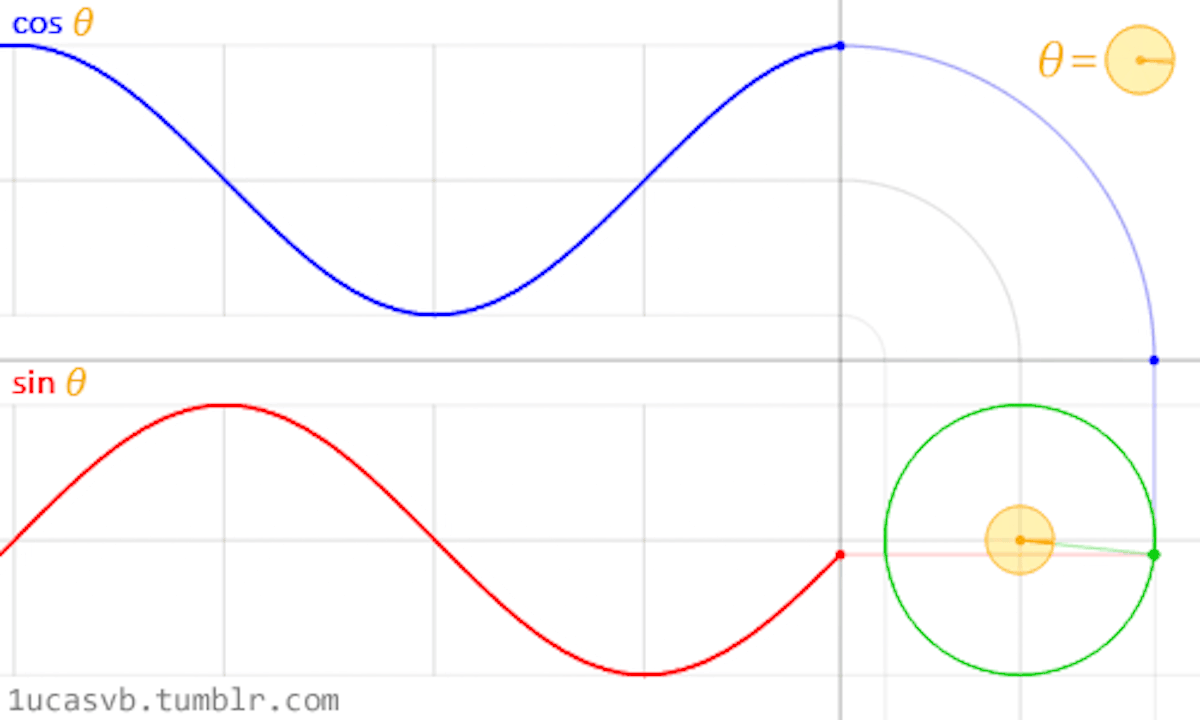
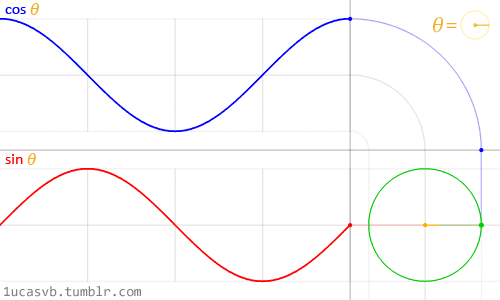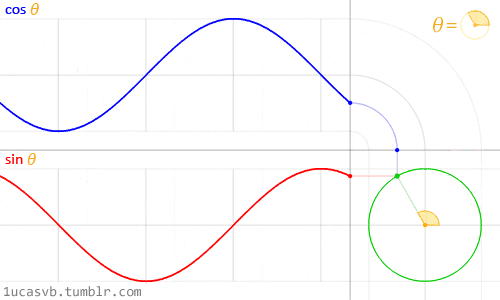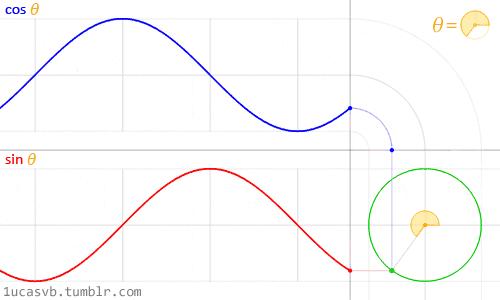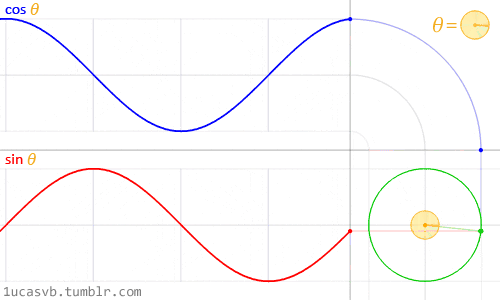
Trigonometries and shaping functions allow us to animate elements whenmanipulated by the constant of time (counter). In combination with shaders, very organic shapes can be created by means of sine and cosine, and slightly rough and edgy forms can be achieved with moduli and fractals (cut elements).Since shaders execute all tasks for each pixel on the screen, these functions becomecrucial in an interplay of the process, allowing to shape the whole canvasinto entirely different directions. Noise functions and existing scrips from computergraphics help us to achieve desired results. Pre-existing knowledge canbe utilised to reverse engineer the work of computer graphics to build uponexisting visuals and create new outcomes.Sine and CosineSine and cosine proved to be of great value when animating, shaping andblending values. These two very essential trigonometric functions work togetherto create very round and organic shapes. Once understood, these twofunctions become very handy in the creative process. It is crucial to understandhow they behave and in what ways they can be combined (Gonzalez Vivo &Lowe, 2015). Gonzalez Vivo & Lowe (2015) explain both functions as follows:
In a nutshell, given an angle (in radians) they will return the correct positionof x and y (sine) of a point on the edge of a circle with a radius equal to 1.Nevertheless, the fact that they return normalized values (values between -1and 1) in such a smooth way makes them an incredible tool.